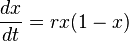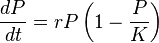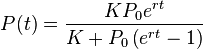Uma coisa que a equação não mostra

É como surge a função logística na análise do mercado.

Temos:

dN/dt = r*N*(1-N/T)

Imagino que este problema pode ser sanado pela introdução de outra variável que poderíamos chamar de penetração no mercado. A penetração pode ser definida como o número de pessoas que tem informações sobre o produto (e pode vir a comprá-lo) dividida pelo número total de pessoas disponível no mercado

x=N/T

Desta forma:

dx/dt=1/T*dN/dt = r*N/T*(1-N/T)

Logo:

dx/dt=r*x*(1-x)

A equação também mostra que ao pensarmos em um sistema baseado em penetração no mercado talvez seja possível elaborar diferentes formas de representar o comportamento da penetração baseado em árvores sociais.

Invariavelmente não há como escapar do termo (1-P), pois ele diz que o mercado só pode crescer enquanto existirem pessoas que não sabem sobre o produto.

Em última análise temos um problema sobre propagação de algo em um grafo. Podemos também considerar como o fluxo de um fluido em um meio poroso, assim a penetração pode ser vista como a "umidade" do meio poroso. Então no fundo temos um problema de difusão:

Claro que resta a questão de como podemos converter isto em:

Aonde claramente x não é uma variável do espaço.

O modo mais simples é considerar o meio homogêneo e calcular a du/dt = d2u/dr2, por exemplo em um disco. A parte da derivada segunda precisa de conversão para penetração.

Isto ainda merece estudos posteriores

Mais umas coisinhas sobre a função logística

Apesar de não ser a única possível, a função logística tem algumas características particularmente interessantes:

a) A derivada é sempre positiva, mas tem um máximo. Isto quer dizer que ela sobe e depois caí
b) O crescimento depende do tamanho do mercado - tanto do mercado ocupado quanto do mercado ainda por ocupar
c) O tamanho do mercado (K) é fixo no modelo logístico.

Na realidade, temos o problema é bem mais complexo do que isto. O mercado é composto de várias seções aonde cada uma delas tem uma capacidade de pagamento. Uma vez esgotada esta capacidade de pagamento o mercado não irá crescer.

Em adição, o tamanho do mercado pode variar no tempo por fatores como crescimento populacional ou descoberta de novas tecnologias, enfim uma variedade de fatores.

Claro que um modelo que preveja ou antecipe todas as possíveis mudanças inesperadas é invíável (mesmo um probabilístico). Então vamos introduzir as mudanças de modo mais gradual. A primeira questão é com relação ao tamanho do mercado - e quanto o mesmo pode pagar.

Uma suposição razoável é que a taxa de variação de preços (dq/dt) seja proporcional ao negativo da taxa de variação do tamanho do mercado (dp/dt).

Assim se dp/dt=a*p(1-p/K) então dq/dt=-b*dp/dt

Mas isto não é suficiente. O preço em q(0) deve ter um valor q0 e o preço quando q(infinito) não pode ser zero. Isto quer dizer que quando dq/dt=0, então q=q(infinito) e q(0)=q0 (em outras palavras a inclinação é zero no início e no fim da curva).

Como fica isto? Bem em um próximo post vou dar uma investigada.

Número de telefones celulares no mundo

Usando novamente a curva logística tive oportunidade de tentar prever como será a evolução do número de telefones celulares no mundo. O método de ajuste parece ter funciona, mas a curva não chega a 6.6 bilhões em uma das estimativas.

Mas vamos as previsões:

Estima 1 Estima 2 Dados
Ano Bilhões Bilhões Bilhões
1990 0,036 0,030 ?
1991 0,048 0,042 ?
1992 0,066 0,058 ?
1993 0,089 0,080 ?
1994 0,121 0,111 ?
1995 0,163 0,153 ?
1996 0,221 0,210 ?
1997 0,297 0,288 0,269
1998 0,398 0,392 0,337
1999 0,530 0,529 0,539
2000 0,702 0,709 0,808
2001 0,921 0,938 1,078
2002 1,195 1,221 1,280
2003 1,528 1,562 1,549
2004 1,922 1,953 1,886
2005 2,371 2,384 2,290
2006 2,861 2,834 2,761
2007 3,372 3,279 3,300
2008 3,882 3,697 ?
2009 4,367 4,071 ?
2010 4,808 4,390 ?
2011 5,192 4,653 ?
2012 5,517 4,863 ?
2013 5,782 5,026 ?
2014 5,993 5,150 ?
2015 6,158 5,243 ?
2016 6,286 5,313 ?
2017 6,382 5,364 ?
2018 6,455 5,401 ?
2019 6,510 5,428 ?
2020 6,551 5,448 ?

Será que irá se tornar verdade?

Quem sabe?

Revisando previsões e criando novas

Após melhorar o cálculo do ajuste (através da minimização da variância) cheguei nos seguintes dados relativos a população:

População Brasileira (Milhões)

Ano Cálculo Medida
2003 178.7 178.
2004 181,1 181.1
2005 183.4 183,4
2006 185.6 185,6
2007 187.6 187,6
2008 189,6 189,8

Extrapolação: 2009 - 191,50 Milhões, para 2010 - 193,29 Milhões. O IBGE prevê estes números como 191.480.630 para 2009 e 193.252.604 para 2010.

Saturação: 222,15 Milhões - 90% deste valor em 2014, 99% em 2049

Se utilizarmos a série da população desde 1948, o ajuste fica mais interessante

Ano Cálculo Medida
2003 179.1632 178
2004 181.5391 181.1
2005 183.8810 183.4
2006 186.1880 185.6
2007 188.4587 187.6
2008 190.6925 189.8

Extrapolação: 2009 - 192,89 Milhões, para 2010 - 195,05 Milhões. O IBGE prevê estes números como 191.480.630 para 2009 e 193.252.604 para 2010.

Mas há outras mudanças:

Saturação: 267,72 Milhões - 90% deste valor em 2040, 99% em 2099

Qual está mais correto? Quem sabe?

Mas esta não é a última previsão. No caso do sistema de energia elétrica a saturação é por volta de 8 TW (TeraWatts). Hoje o mesmo se encontra na vizinhança dos 60 GW. Segundo o ajuste logístico.

No ano de 2008 o valor projetado foi de 62.5 GW (comparado com 62.6 GW medidos). Em 2009, o valor projetado é de 64.5 GW e em 2010 este valor é de 66.5 GW.

No entanto observando os dados do ONS, há uma clara indicação que o valor de 2009 será provavelmente abaixo do de 2008 (devido a crise). Isto pode mudar, mas já indica uma característica do tipo de dado que o ajuste logístico desconsidera: fatores exógenos ao processo.

Isto quer dizer que a previsão é boa desde que não acontece nada fora da dinâmica atual do sistema. Uma crise econômica não é algo previsto na dinâmica do sistema.

Ainda assim, vale a pena fazer alguns estudos. Se eu comprar 1 ação de companhia elétrica por R$ 1,00, quanto tempo leva para dobrar o meu capital?

Isto pode ser predito pelo modelo logístico - assumindo o aumento do consumo como única variável. Portanto, assumindo que este R$ 1,00 foi aplicado em 2008 (62.5 GW), basta verificar quando teremos 123 GW de consumo. Isto é por volta de 2030.

Logo temos uma valorização de 100% em 21 anos - uma taxa de 3.3% ao ano. Isto não é nada estelar. Mas ao fazermos o mesmo investimento no negócio de carvão vegetal, o retorno será em "apenas" 917 anos.

Esta é uma grande vantagem do modelo logístico - previsão de longo prazo. Em um sistema com mercado finito, como o modelado pelo modelo logístico vale a pena usá-lo para tentar encontrar pontos com crescimento mais acelerado.

Depois vamos ver alguns destes

Previsões e previsões

Baseado no modelo corrigido da sigmóide e usando uma técnica de mínimos quadrados em conjunto com um estudo da curva de variância mínima chegamos ao seguinte ponto:

PIB Brasileiro (trilhões de US$)
Ano Cálculo Medida
2003 0,5540 0,5372
2004 0,6640 0,6924
2005 0,8820 0,8776
2006 1,0890 1,0906
2007 1,3340 1,3254
2008 1,5730 1,5727

Extrapolação: 2009 - 1.8208 Trilhões de US$, para 2010 - 2,0579 Trilhões de US$

Saturação: 3,1775 Trilhões - 90% deste valor em 2015, 99% em 2023

Naturalmente isto supõe que as coisas continuem funcionando mais ou menos como estão nos próximos 6 a 14 anos.

População Brasileira (Milhões)

Ano Cálculo Medida
2003 178.7 178.9
2004 181,1 181.1
2005 183.4 183,3
2006 185.6 185,4
2007 187.6 187,6
2008 189,6 189,8

Extrapolação: 2009 - 191,963 Milhões, para 2010 - 194,1421 Milhões

Saturação: 383,02 Milhões - 90% deste valor em 2105, 99% em 2221

Depois vamos ver o que funcionou ou não

Transformação não linear

Neste caso consideramos que os pontos que possuímos tem uma configuração do tipo

y=A*tanh(b*x)

Temos que fazer uma transformação inversa, assim:

tanh(b*x)=y/A

Logo:

x=1/b*atanh(y/A)

Isto resulta em:

x=1/(2*b)*ln[(1+y/A)/(1-y/A)]

Comparando com a transformação logaritimica:

y=A*exp(b*x)

ln(y)=ln(A)+b*x

O problema mais premente é como determinar A. Infelizmente A é um fator de escala - a priori PARECE que não é fácil de ser identificado. Mas sabemos algumas coisas, entre elas é que A é maior ou igual ao maior valor de y. Podemos com uma certa tranquilidade fazermos o seguinte estudo:

1) Fazemos o cálculo para A=ymax
2) Fazemos o cálculo para A=2*ymax
3) Fazemos o cálculo para A=4*ymax
4) Fazemos o cálculo para A=8*ymax

Destes resultados cálculamos os resíduos da curva. O melhor ajuste terá os menores resíduos. A conta que devemos fazer é:

Y=1/2*ln[(1+y/A)/(1-y/A)]=b*x

Então tendo esta formulação:

b=inv(x'*x)*x'*y

Mas o ponto interessante é que funciona de uma forma até bem robusta

Acertando a curva

Ao pensar no problema da curva me veio uma idéia interessante.

Ao fazermos um ajuste polinomial geralmente usamos o método dos mínimos quadrados.

No caso se queremos ajustar uma série de pontos a uma curva do tipo:

a*(1-exp(-b*x))

teremos somente dois parâmetros a determinar, mas com a complexidade que temos uma situação não linear. E sem sabermos quem é b como resolver o problema?

Bem, se expandirmos a exponencial em série teremos:

a*b*x+(-1/2*a*b^2)*x^2+1/6*a*b^3*x^3+(-1/24*a*b^4)*x^4+1/120*a*b^5*x^5

Vamos limitar em ordem 3:

a*b*x+(-1/2*a*b^2)*x^2

Chamando a*b de a1, a*b^2 de a2 temos agora:

a1*x+(-1/2*a2)*x^2

Então sabemos que b=a2/a1 e a=a1^2/a2, assim temos um modelo razoável de mínimos quadrados a partir de uma aproximação polinomial.

Infelizmente, o funcionamento parece ser menos do que estelar. Talvez com a introdução de novas condições o sistema possa melhorar.

Outros modelos

A equação de Lotka-Volterra não é o único modelo de competição com recursos finitos.

Um outro modelo é o exponencial:

dp/dt=a*(1-p/K)

E outro é Rayleigh

dp/dt = t/s^2*(1-p/K)

Na realidade, pelo que vi os modelos do tipo

dp/dt=m(t)*(1-p/K) satisfazem os requisitos do crescimento limitado

Já como definir qual dos modelos satisfaz a formulação genérica é algo substancialmente mais delicado. Da minha parte, acredito que a solução só será possível com várias análises de caso.

Entretanto, a formulação de Rayleigh, exponencial e logística já me indicaram alguns detalhes:

1) A formulação de Rayleigh parece ter a maior taxa de subida, apesar de um certo atraso no início

2) A formulação exponencial tem o início mais rápido e o final mais lento

3) A formulação logística parece ser a intermediária.

Outro ponto que me chamou a atenção é que a priori qualquer distribuição contínua pode ser utilizada no cálculo de funções limitantes. por exemplo:

p(t) =t^n/(1+t^n)

A EDO neste caso é:

dp/dt=n/t*p*(1-p/K)

Uma questão é como se comporta a derivada em todos os casos. Ela atinge um máximo e depois diminui até zerar. Se considerarmos p como mercado, o que significa dp/dt?

Imagino que seja a taxa de variação do mercado. Assim, temos primeiro um crescimento bastante grande no mercado até um ponto de máxima taxa de crescimento - depois esta taxa diminui até alcançar zero (que corresponde a totalidade do mercado).

Em todos os modelos há uma componente (1-p/K) que determina em parte a taxa de crescimento. Esta componente vai diminuindo a medida que p se aproxima de K (mercado disponível). Nos modelos de Rayleigh e exponencial, podemos dizer que a taxa diminui porque o tamanho do mercado diminui.

O comportamento do logístico é similar, mas há dois fatores em consideração p e (1-p/K). E somente o produto dos dois é que determina a taxa de crescimento. Enquanto p é pequeno, (1-p/k) pode ser grande, mas o produto é determinado por p pequeno.

Já quando (1-p/K) é pequeno, p pode ser grande - mas (1-p/K) que determinará o crescimento.

De qualquer maneira é o tamanho remanescente do mercado (1-p/K) que determina o crescimento no longo prazo. E isto é um ponto pra lá de importante pois implica que dado um preço constante, a taxa de crescimento das vendas após o pico irá sempre diminuir.

Estimando o tamanho do mercado

Após algumas manipulações cheguei a uma formulação que permite estimar o tamanho do mercado. Essencialmente, considerando um processo discreto temos que:

K(k)=(p(k)^3-p(k-1)*p(k)^2-p(k-1)^2*p(k+1)+p(k-1)^2*p(k))/(p(k)^2-p(k-1)*p(k+1));

Após alguns testes verifiquei que realmente o valor do mercado era encontrado.

Mas existem alguns problemas:

- A fórmula é sensível ao ruído, portanto flutuações aleatórias causam erros no cálculo do tamanho do mercado

- Ao se usar a fórmula, temos que pode-se estimar qual o lucro possível que um determinado investimento tem naquele mercado - e também seu preço. Alterações no perfil de preços irão causar alterações no mercado.

Ao tentar "prever" o mercado de Santa Catarina chegamos a dois resultados diferentes:

1,315 TWh e 1,269 TWh

Naturalmente além das variações naturais da série histórica existe a questão de quem é k-1, k e k+1.

Outro exemplo: previsão de mercado de consumo residêncial da Light - 7.73 GWh (atual 7.214)

Mais um exemplo: previsão de mercado de consumo industrial AT - 813 MWh (atual 412)

Outro exemplo já do atlas de energia: eletricidade 51 a 55 kteps (em 2007 35 kteps)

Infelizmente, como saber qual o tamanho real?

Cotação

O modelo anterior permitiu algumas simulações interessantes.

E o ponto mais curioso é a similaridade entre a curva de cotação de um ação e a curva obtida com o modelo.

Ainda resta é claro a questão da estimação de K/P0 pelos diversos investidores. Mas neste modelo é claro que uma vez que o mercado total seja atingido, acabam as variações estatísticas.

Neste exemplo a taxa r foi considerada uma variável aleatória com média 0.125 e um desvio padrão de 2.5. Isto implica em uma larga variação da ação - ou da venda do bem - ao longo do tempo.

Um problema neste modelo é como estimar o K/P0. A primeira vista a forma de calcular K/P0 apresentada no post anterior não parece ter muita utilidade. Em adição, a derivada numérica não parece ajudar muito no cálculo deste valor.

Ainda assim, aparentemente temos um modelo muito mais próximo do funcionamento real de uma ação do que tinhamos anteriormente. O modelo é essencialmente um modelo baseado no mercado. O preço da ação na forma atual é definido exclusivamente pela taxa de aumento da fatia de mercado.

Ainda resta incluir no modelo um método para estimar o tamanho do mercado.

A questão da estimação

Se formos olhar as equações anteriores, podemos simplificar parte do pepino considerando K/P0.

Isto é na realidade a capacidade de crescimento dado um mercado sem concorrentes. Em teoria, neste caso K/P0 indica exatamente quanto será o faturamento da empresa baseado no faturamento inicial.

Assim uma estimativa deste valor pode indicar um bom investimento de um investimento muito ruim. Claro que estamos assumindo que o mercado é que irá gradativamente (segundo a taxa r) comprar o produto.

Nestas condições

r/(r-1/p(t)*dp/dt)

é uma aproximação de K/P0

No entanto alguns problemas continuam:

a) Como determinar r
b) Como determinar dp/dt

r é essencialmente uma variável aleatória. E por este motivo já complica bastante o barco.

Já 1/p*dp/dt é exatamente r para uma aproximação de crescimento exponencial - o que obviamente não é verdade. Então pequenos erros na determinação de r ou de 1/p*dp/dt podem levar a subestimar ou sobrestimar K/P0.

E como se já não fosse complicação suficiente, podemos dizer que o valor esperado de r é exatamente 1/p*dp/dt (pelo menos enquanto p/K for pequeno - ou seja na fase de crescimento).

Talvez valha a pena testar algumas simulações deste problema

Dinâmica na distribuição

Um ponto que vale a pena explorar é a dinâmica da distribuição. Neste caso temos um recurso finito (mercado) sendo explorado. Então temos um modelo Lotka-Volterra competitivo:

Naturalmente, K é a capacidade do meio em sustentar. Quando x=K então a taxa de crescimento torna-se nula. Neste modelo K seria o tamanho do mercado disponível.

r é a taxa de crescimento per capita.

Em uma situação mais genérica poderíamos ter diversas empresas competindo pelo mesmo mercado. Naturalmente, o resultado seria "market-shares" diferenciados para cada uma delas, compondo o mercado final.

Mas ainda é mais complexo - a taxa de crescimento deve ser modelada como uma variável aleatória, e K pode não ser conhecido exatamente (só de modo aproximado) ou mesmo variar no tempo.

Mas no caso em que K não varia no tempo a solução da equação é:

Este tipo de solução é algo da família das tangentes hiperbólicas. O interessante é que há uma fase de crescimento e por fim uma de estagnação - aonde não se verificam crescimentos.

Entretanto, talvez tão interessante quanto o comportamento dinâmico é quando se associa a taxa de crescimento r a uma estimativa de K. Esta estimativa pode ser a grosso modo encontrada pela série de Taylor da exponencial.

Desta forma

P(t0)=K*P0*exp(r*t0)/(K+P0*(exp(r*t0)-1))
P(t1)=K*P0*exp(r*t1)/(K+P0*(exp(r*t1)-1))

P(t1)/P(t0)=exp(r*(t1-t0))*(K+P0*(exp(r*t0)-1))/(K+P0*(exp(r*t1)-1))

Aproximando por Taylor para r pequeno:

P(t1)/P(t0)=1+(K-P0)*(t1-t0)/K*r

Resolvendo para K

Seja x=P(t1)/P(t0)

K=(t1-t0)*r*P0/(1+(t1-t0)*r-x)=P0/(1+(1-x)/[(t1-t0)*r])

Naturalmente, neste modelo é importante saber o valor de r (e o mesmo deve ser pequeno)

Outras distribuições de renda

Vamos ver o efeito de algumas distribuições de renda no faturamento.

A primeira é uma do tipo p0/(1+x^n)

O faturamento é dado por:

p0*x/(1+x^n)

O máximo desta função é em

x=(-1+n)^(-1/n)

Para n=2, o máximo de faturamento ocorre em x=1 com p=p0/2. O faturamento total é de 0.5*p0

Para n=3, o máximo de faturamento ocorrem em x=0.7937005260 com p=2/3*p0, o faturamento total é de 0.53*p0

Para n=4, o máximo de faturamento ocorrem em x=0.7598356857 com p=3/4*p0, o faturamento total é de 0.57*p0

Para n=5, o máximo de faturamento ocorrem em x=0.7578582833 com p=4/5*p0, o faturamento total é de 0.51*p0

Para n=6, o máximo de faturamento ocorrem em x=0.7647244913 com p=5/6*p0, o faturamento total é de 0.64*p0

Para n=7, o máximo de faturamento ocorrem em x=0.7741685699 com p=6/7*p0, o faturamento total é de 0.66*p0

Para n=8, o máximo de faturamento ocorrem em x=0.7840842767 com p=7/8*p0, o faturamento total é de 0.69*p0

Para n=9, o máximo de faturamento ocorrem em x=0.7937005260 com p=8/9*p0, o faturamento total é de 0.71*p0

Para n=10, o máximo de faturamento ocorrem em x=0.8027415618 com p=9/10*p0, o faturamento total é de 0.72*p0

Como pode ser visto, um fenômeno interessante ocorre na passagem de n=4 para n=6. O número médio de pessoas x aumenta. Isto provalmente está ligado ao número de raízes e quais raízes são escolhidas.

Em todos os modelos, quando x=1, temos que p=p0/2; este será o máximo que pode ser coberto no sistema (x=1). Todos os valores estarão ligados a quão rápido a distribuição de renda cai de x=0 para x=1.

É interessante notar que quanto maior n, mais equitativa a distribuição de renda se torna.

E claro, maior o faturamento para a empresa...

Usando o modelo anterior

Com os dados p0=100, p1=10 e n1=500 podemos descobrir aonde ocorre o maior faturamento.

Neste caso, o faturamento máximo é de 13911.15620

E ele ocorre quando n=277.7222222

O preço por unidade p é de 50.09018036

Isto é interessante, pois neste modelo de classes sociais (trapezoidal), o maior faturamento não ocorreu com n=250 e preço p=50.

Claro de p1 dobrar então o maior faturamento é de 15643.79008. E ele ocorre com n=312.3750000 e p=50.08016032

Claro de p0 dobrar e p1=10 então o maior faturamento é de 26363.25309. E ele ocorre com n=263.1315789 e p=100.1903808

Ao se aumentar p0, temos que o faturamento cresce mas o número de pessoas atendidas diminui. Mudando a inclinação do trapézio através do aumento no número de pessoas teremos certamente maior faturamento e o preço é aproximadamente metade do valor inicial.

É interessante que quanto menor a diferença de preço entre p0 e p1, maior é o número de pessoas atendidas. Como p1 é dado pela capacidade de pagamento das pessoas, então é interessante que os custos sejam os mais baixos possíveis para realizar isto - é do interesse do produtor obter o maior lucro.

E este modelo mostra que o maior lucro é obtido servindo ao maior número de pessoas.

E o lucro com a pirâmide social?

Um ponto interessante do post anterior é que existe um estímulo de diminuir custos para conquistar mercados e aumentar o lucro.

A análise foi feita baseada em degraus discretos. Mas como fica com uma curva mais suave?

Podemos aproximar a pirâmide da seguinte forma preço x número de pessoas. Começando em um p0 com 0 pessoas e terminando com um p1 com n1 pessoas. Isto resulta, caso seja realizada uma queda linear em um trapézio.

Vamos considerar um preço por unidade p0 e chegando até um preço por unidade p1. O preço p0 é o preço que o mais rico da cidade está disposto a pagar e o preço p1 é o preço que o mais pobre da cidade está disposto a pagar.

- Com p0 apenas 1 pessoa compra a mercadoria
- Com p1, n1 pessoas compram a mercadoria

Podemos escrever a relação entre preço e número de pessoas da seguinte forma:

1 = a*p0+b
n1=a*p1+b

Logo a=(n1-1)/(p1-p0)

E b=1-(n1-1)/(p1-p0)*p0

Assim a fórmula para o número de pessoas em relação ao preço por unidade é:

n=1+(n1-1)*(p-p0)/(p1-p0)

Como exemplo: p0=100, p1=10 e n1=500

Logo n=1+499*(100-p)/(100-10) = 4999/9-499/90*p

Depois vamos ver como isto pode ser maximizado e como se relaciona com o lucro

Menos lucro é mais lucro

A verdade é que o mercado, como já foi visto define em termos o preço máximo. Se temos os custos, digamos R$ 166,67 por pessoa, ao definirmos as faixas de consumo podemos mais ou menos estimar o preço de uma mercadoria.

No caso:
- Se a mercadoria custar R$ 389,34 então terá somente um mercado potencial de 530 mil pessoas. Considerando o custo temos um lucro de R$ 222,67 por pessoa, totalizando R$ 118 milhões de lucro final.

- Se a mercadoria custar R$ 262,55 então terá um mercado potencial de 2,65 milhões de pessoas. Considerando o custo temos um lucro de R$ 95,88 por pessoa, totalizando R$ 254 milhões de lucro final.

Do ponto de vista de mercado então é mais lógico que a mercadoria custe R$ 262,55 e tenha um lucro por unidade menor.

Isto é um exemplo de um caso claro aonde a diminuição do lucro por unidade leva a um aumento do lucro final - devido ao mercado ampliado.

O que leva a investigar: O que aconteceria se o custo fosse de R$ 98,50 ao invés de R$ 166,67.

Neste caso, não vale a pena baixar o preço até R$ 139,17. O lucro com o preço de R$ 389,34 é de R$ 154 milhões; já com o preço de R$ 262,55 o lucro é de R$ 434 milhões. Mas ao diminuirmos o preço para R$ 139,17 o lucro passa a ser de R$ 301 milhões.

Já se o custo cair a R$ 50,00, o valor de venda que proverá maior lucro é de R$ 89,17 a unidade (lucro final de R$ 661 milhões).

A importância desta análise é mostrar que a definição do que é a melhor margem de lucro não pode ser obtida sem um estudo do mercado. E isto é algo que a análise da teoria de valor de Marx deixa a desejar

O custo aluno

Agora sabemos que o tamanho do mercado global para o setor do ensino fundamental é de R$ 38,5 bilhões, sendo distribuídos da seguinte forma:

Classe A1 206 milhões (R$ 389,00/aluno a cada mês ou )
Classe A2 556 milhões (R$ 262,55/aluno)
Classe B1 663 milhões (R$ 139,17/aluno)
Classe B2 640 milhões (R$ 80,51/aluno)
Classe C1 531 milhões (R$ 47,78/aluno)
Classe C2 338 milhões (R$ 29,05/aluno)
Classe D 257 milhões (R$ 19,40/aluno)
Classe E 17 milhões (R$ 11,07/aluno)

Por um estudo do INEP é possível determinar os custos para realizar o ensino médio. E o resultado médio é de R$ 2.000,00 po ano - ou R$ 166,67 por mês.

A composição destes custos é:
55% Docentes - R$ 91,67/aluno por mês
28% Funcionários - R$ 46,67/aluno por mês
6% Insumos
8% Material de Consumo
3% Material Permanente

Portanto a rúbrica pessoa é responsável por 83% do custo-aluno. Por outra metodologia chega-se a um percentual de 73%. De qualquer modo, fica claro que o maior fator no custo-aluno é o custo do pessoal.

Já o poder de pagamento de cada uma das classes sociais pode ser ponderado no parâmetro de um poder de pagamento médio ou uma mensalidade média. Este valor é de R$ 60,60

Este seria o valor da mensalidade média considerando um pagamento diferenciado por classe social. Mas é interessante verificar quanto fica o valor R$ 106,07 abaixo do valor dado pelo custo-aluno calculado pelo INEP.

Um modo de tornar isto mais barato é diminuir os custos com docentes e funcionários. Caso estes custos sejam diminuídos pela metade temos que o custo-aluno caí para R$ 98,50. E isto faz com que o valor abaixo do valor dado por custo aluno fique apenas R$ 98,50.

E como isto ajuda na solução do problema da educação?

Bem, tem um jeito.

Se o governo financiar parte do deficit para a escola, então o problema pode ser resolvido. Primeiro sabemos o custo-aluno. Este pode ser arredondado para R$ 170 sem perda de generalidade. Então as classes B1 até E precisariam de uma compensação:

Classe A1 R$ 0,00
Classe A2 R$ 0,00
Classe B1 R$ 27,60
Classe B2 R$ 86,16
Classe C1 R$ 118,89
Classe C2 R$ 137,62
Classe D R$ 147,27
Classe E R$ 155,60

Isto dá um total anualizado de R$ 71 bilhões considerando o número de alunos a serem educados. Este valor pode ser grandemente diminuído se as proporções de gastos com a educação por família aumentarem de 4% para 8% (R$ 48 bilhões) ou mesmo ainda menor se a variação subir de 4% para 16% (R$ 23 bilhões). Neste último caso teríamos:

Classe A1 R$ 0,00
Classe A2 R$ 0,00
Classe B1 R$ 0,00
Classe B2 R$ 0,00
Classe C1 R$ 0,00
Classe C2 R$ 50,47
Classe D R$ 89,07
Classe E R$ 122,40

Naturalmente, isto implica em descontos pagos a escola. Em termos simples, poderíamos ter mensalidades definidas pelas escolas baseadas no custo-aluno e complementação governamental para os casos comprovadamente de baixa renda.

Mais educação de mercado

Temos então um mercado de r$ 65 bi anual no Brasil. Este é o mercado da educação.

Além disto temos a composição de gastos do brasileiro médio:

Alimentação: 18%
Habitação: 30%
Transporte: 9%
Assistência Médica: 6%
Vestuário: 5%
Educação: 4%
Higiene: 2%
Recreação: 2%

E uma composição de recursos por classe social no Brasil:

Classe A1 R$ 9.733,47
Classe A2 R$ 6.563,73
Classe B1 R$ 3.479,36
Classe B2 R$ 2.012,67
Classe C1 R$ 1.194,53
Classe C2 R$ 726,26
Classe D R$ 484,97
Classe E R$ 276,70

E assim podemos ter uma idéia do tamanho de gastos na educação:

Classe Soc. Mês Ano
Classe A1 R$ 389,34 R$ 4.672,07
Classe A2 R$ 262,55 R$ 3.150,59
Classe B1 R$ 139,17 R$ 1.670,09
Classe B2 R$ 80,51 R$ 966,08
Classe C1 R$ 47,78 R$ 573,37
Classe C2 R$ 29,05 R$ 348,60
Classe D R$ 19,40 R$ 232,79
Classe E R$ 11,07 R$ 132,82

Então para famílias, este valor pode ser dobrado. Isto é claro considerando que pai e mãe sejam provedores econômicos.

E naturalmente, temos de ter ainda uma noção do número de filhos e sua distribuição por classe social. Mas os dados que temos é que é algo em torno 2.5 e 2.8 crianças (nas classes A, B e C). Vamos considerar as seguintes taxas:

Classe Soc. Fecundidade Percentual
Classe A1 0,8 1
Classe A2 1,2 4
Classe B1 2,2 9
Classe B2 1,9 15
Classe C1 2,15 21
Classe C2 2,2 22
Classe D 2,8 25
Classe E 5 3

Isto resulta em uma taxa de 2,3 (o que é próxima da real). Assim de cada 10 famílias da classe A1 vemos 8 filhos e 20 país, ou seja a família na classe A1 é composta por 2,8 pessoas (sendo 0,8 o efeito da prole). Em termos simples, do total de membros da classe A1, se considerarmos que os pais já possuem nível educacional completo teremos:

0,8/2,8 = 0,29 ou 29% dos membros pertence a prole.

Segundo a mesma lógica

Classe Soc. Percentual filhos Percentual global Números (milhões)
Classe A1 28,57 0,286 0,57
Classe A2 37,5 1,500 3
Classe B1 52,38 4,714 9,43
Classe B2 48,72 7,308 14,62
Classe C1 51,81 10,880 21,76
Classe C2 52,38 11,524 23,05
Classe D 58,33 14,583 29,17
Classe E 71,43 2,143 4,29
105,87

Então temos:

- Classe A1: 570 mil alunos
- Classe A2: 3 milhões de alunos
- Classe B1: 9.43 milhões de alunos
- Classe B2: 14.62 milhões de alunos
- Classe C1: 21.76 milhões de alunos
- Classe C2: 23.05 milhões de alunos
- Classe D: 29.17 milhões de alunos
- Classe E: 4,29 milhões de alunos

Isto resulta em um total de 105 milhões de alunos. Na realidade, o número do censo

De 0 a 7: 33,69 milhões
De 7 a 15 anos (ensino fundamental): 38,5 milhões
De 15 a 18 anos (ensino médio): 14,4 milhões
De 18 a 22 anos (ensino superior): 19,25 milhões

Comparado com os dados medidos temos cerca de 56,3 milhões que estudam, sendo que 5 milhões estão no ensino superior. Portanto o ensino médio + fundamental consistem de 51 milhões de pessoas.

Comparado com nossa estimativa temos: 52,94 milhões. A diferença maior surge no ensino superior, aonde apenas 25% das pessoas originalmente habilitadas chegam a participar

Mas dos 53 milhões, podemos estimar o tamanho dos mercados:

Classe Soc. Números (milhões)
Classe A1 0,53
Classe A2 2,12
Classe B1 4,77
Classe B2 7,95
Classe C1 11,13
Classe C2 11,66
Classe D 13,25
Classe E 1,59

O tamanho do mercado global para este setor é de R$ 38,5 bilhões, sendo distribuídos da seguinte forma:

Classe A1 206 milhões (R$ 389,00/aluno)
Classe A2 556 milhões (R$ 262,55/aluno)
Classe B1 663 milhões (R$ 139,17/aluno)
Classe B2 640 milhões (R$ 80,51/aluno)
Classe C1 531 milhões (R$ 47,78/aluno)
Classe C2 338 milhões (R$ 29,05/aluno)
Classe D 257 milhões (R$ 19,40/aluno)
Classe E 17 milhões (R$ 11,07/aluno)

Claro que estes valores são mensais. De qualquer modo é interessante ver que o único modo de manter este tipo de serviço é diminuindo as despesas por aluno.

Mais a frente vamos ver como isto pode ser feito, agora que temos o tamanho do mercado, quais os participantes do mercado e quanto cada um pode gastar com o serviço.

Educação como Negócio

Na análise feita percebe-se que o tamanho do mercado de educação no Brasil beira 65 bilhões se observarmos o mesmo anualizado.

Um parcela relativamente pequena corresponde ao ensino superior.

Dada a situação econômica do país e considerando 6 milhões de interessados, temos as seguintes estatísticas de mensalidades possíveis:

60 mil alunos tem condições de pagar mensalidades acima de R$ 1.946,69
240 mil alunos tem condições de pagar mensalidades acima de R$ 1.312,75 e abaixo de R$ 1.946,69
540 mil alunos tem condições de pagar mensalidades acima de R$ 695,87 e abaixo de R$ 1.312,75
900 mil alunos tem condições de pagar mensalidades acima de R$ 402,53 e abaixo de R$ 695,87
1,26 milhões de alunos tem condições de pagar mensalidades acima de R$ 238,91 e abaixo de R$ 402,53
1,32 milhões de alunos tem condições de pagar mensalidades acima de R$ 145,25 e abaixo de R$ 238,91

E claro que isto continua até a classe E. A média da mensalidade nesta situação é de R$ 303,02

Quais são os mercados neste caso?

-O mercado A1 tem potencial para R$ 116 milhões (60 mil alunos - 1.4 bi/ano)
-O mercado A2 tem potencial para R$ 315 milhões (240 mil alunos - 3.8 bi/ano)
-O mercado B1 tem potencial para R$ 375 milhões (540 mil alunos - 4.5 bi/ano)
-O mercado B2 tem potencial para R$ 362 milhões (900 mil alunos - 4.3 bi/ano)
-O mercado C1 tem potencial para R$ 301 milhões (1,26 milhões de alunos - 3.6 bi/ano)
-O mercado C2 tem potencial para R$ 191 milhões (1,32 milhões de alunos - 2.3 bi/ano)
-O mercado D tem potencial para R$ 145 milhões (1,5 milhões de alunos - 1.7 bi/ano)
-O mercado E tem potencial para R$ 10 milhões (180 mil alunos - 119 milhões/ano)

Claramente o filet-mignon é a classe A com faturamento de 5.2 bi/ano tendo 300 mil alunos (anualidade de 17.3 mil). Em seguida vemos a classe B com faturamento de 8.8 bi/ano e 1,44 milhões de alunos (anualidade de 6,11 mil).

Se mantivermos 30 alunos por professor, a primeira alternativa implica em 10 mil professores. Se os mesmos tiverem um salário de 10 mil, ao longo do ano teremos um custo de 1.2 bi.

Já na segunda alternativa tem-se 48 mil professores. Considerando um salário de 10 mil, tem-se 5.76 bi/ano de salário - ou seja come-se quase todo o lucro.

Mas se juntarmos as duas alternativas, temos 1.74 milhões de alunos ao faturamento de 14 bi/ano. Neste cenário pode-se ter 58 mil professores ganhando 10 mil cada a um custo de 6.96 bi/ano

A anualidade seria de R$ 8,05 mil - o que corresponderia a uma mensalidade de R$ 670,00

Isto é interessante pois desmitifica alguns pontos normalmente defendidos em debates.

Tamanho anualizado

Achei que seria interessante colocar o tamanho do mercado já anualizado.

Setor Mercado Anual (R$ Bilhões)
Alimentação: 294,54
Habitação: 490,89
Transporte: 147,27
Assistência Médica: 98,18
Vestuário: 81,82
Educação: 65,45
Higiene: 32,73
Recreação: 32,73

Mercado anualizado R$ 1,2 trilhões

Tamanho do Mercado Brasileiro

Após estudar um pouco sobre a população economicamente ativa e os gastos que as pessoas fazem, creio que é possível realizar algumas estimativas educadas sobre a população.

Estas estimativas permitem determinar de modo aproximado o tamanho do mercado interno para diversos itens. Assim temos para uma população economicamente ativa de 90 milhões

Cenário 1: Recursos médios mensais R$ 1.515,10

Alimentação - tamanho do mercado mensal: R$ 24,54 bilhões
Habitação - tamanho do mercado mensal: R$ 40,91 bilhões
Transporte - tamanho do mercado mensal: R$ 12,27 bilhões
Assistência médica - tamanho do mercado mensal: R$ 8,18 bilhões
Vestuário - tamanho do mercado mensal: R$ 6,82 bilhões
Educação - tamanho do mercado mensal: R$ 5,45 bilhões
Higiene - tamanho do mercado mensal: R$ 2,73 bilhões
Recreação - tamanho do mercado mensal: R$ 2,73 bilhões

Cenário 2: Recursos médios mensais R$ 2.533,55

Alimentação - tamanho do mercado mensal: R$ 41,04 bilhões
Habitação - tamanho do mercado mensal: R$ 69,41 bilhões
Transporte - tamanho do mercado mensal: R$ 20,52 bilhões
Assistência médica - tamanho do mercado mensal: R$ 13,68 bilhões
Vestuário - tamanho do mercado mensal: R$ 11,4 bilhões
Educação - tamanho do mercado mensal: R$ 9,12 bilhões
Higiene - tamanho do mercado mensal: R$ 4,56 bilhões
Recreação - tamanho do mercado mensal: R$ 4,56 bilhões

Em 2008 o faturamento das empresas de alimento foi de R$ 265 bilhões. Isto corresponde a um mercado mensal de R$ 22,08 bilhões (que é próximo dos R$ 24,64 bilhões projetados).

Em 2008, o setor téxtil (que é apenas uma das partes do setor de vestuário) teve um faturamento anual de R$ 43 bilhões (R$ 3,58 bilhões mensais).

Em 2008, o setor de higiene, cosméticos e limpeza teve um faturamento de R$ 22 bilhões. Isto corresponde a um mercado mensal de R$ 1,83 bilhões (que é próximo dos R$ 2,73 bilhões projetados). Mas segundo outros dados em 2007, os consumidores brasileiro gastaram cerca de R$ 43 bilhões (infelizmente não sei em qual crer)

Em 2007, o setor de assitência médica e hospitala teve faturamento próximo R$ 84 bilhões. Isto corresponde a um mercado mensal de R$ 7 bilhões (que é próximo dos R$ 8,18 bilhões projetados).

O importante é que parece que este instrumento permite determinar de modo aproximado o tamanho do mercado.

Sobre o mercado

Como o modelo econômico mostrou, o lucro está intrinsecamente ligado ao mercado. Na realidade, a possibilidade de crescimento do lucro é delimitada pelo mercado.

Então vamos considerar um caso de um mercado em expansão. Ou seja, o objetivo é aumentar o percentual de pessoas que adquirem determinada mercadoria ou produto. Para simplificar vamos evitar a questão do mercado já completado e só considerar um possível mercado em expansão.

Assim, o primeiro passo é saber:

a) Quantas pessoas possui o seu mercado
b) Quanto estas pessoas estão dispostas a gastar com o produto

Bem, um instrumento para isto é a divisão em classes sociais. Isto permite definir algumas noções de preço, quantas pessoas estão habilitadas a fazer parte do mercado e o alcance do produto.

Aqui no Brasil temos uma divisão aproximada:

CLASSE A1 - 1% da população, e renda média mensal familiar a partir de R$ 9.733,47;
CLASSE A2 – 4% da população, renda entre R$ 6.563,73 e R$ 9.733,47;
CLASSE B1 – 9% da população, renda entre R$ 3.479,36 e R$ 6.563,73;
CLASSE B2 -15% da população, renda entre R$ 2.012,67 e R$ 3.479,36;
CLASSE C1 – 21% da população, renda entre R$ 1.194,53 e R$2.012,67;
CLASSE C2 – 22% da população, renda entre R$ 726,26 e R$ 1.194,53;
CLASSE D – 25% da população, renda entre R$ 484,97 e R$ 726,26; e,
CLASSE E – 3% da população, renda entre R$ 276,70 e R$ 484,97.

Os dados são do Olhar 360.

Além disto temos de observar como se gastam os recursos. Na média temos o seguinte:

Alimentação: 18%
Habitação: 30%
Transporte: 9%
Assistência Médica: 6%
Vestuário: 5%
Educação: 4%
Higiene: 2%
Recreação: 2%

Isto dá cerca de 76% do rendimento
Aumento de ativo (poupança e etc): 10%
Diminuição do passivo: 2%
Outras despesas: 12%

Com estes dados podemos colocar o produto e ver quanto é possível de gastos. Um bem relativamente caro como um carro pode ser considerado como aumento do ativo e também transporte - ou seja 20% do orçamento. Portanto teríamos que analisar o custo ao longo de uma sequência de prestações.

Considerando um período de 5 anos teríamos 60 meses e portanto poderíamos estimar como as devidas classes poderiam participar na compra de um carro.

CLASSE A1 - 1% da população, carros acima de R$ 116.802,00
CLASSE A2 – 4% da população, Prestações de até R$ 1946,70 - carros na faixa de R$ 116.802,00;
CLASSE B1 – 9% da população, Prestações de até R$ 1313,46 - carros na faixa de R$ 78.806,00;
CLASSE B2 -15% da população, Prestações de até R$ 695,88 - carros na faixa de R$ 41.752,00; CLASSE C1 – 21% da população, Prestações de até R$ 402,52 - carros na faixa de R$ 24.150,00;
CLASSE C2 – 22% da população, Prestações de até R$ 239,06 - carros na faixa de R$ 14.342,00;
CLASSE D – 25% da população, Prestações de até R$ 145,24 - carros na faixa de R$ 8.714,00; CLASSE E – 3% da população, Prestações de até R$ 97,00 - carros na faixa de R$ 5.820,00.

Bem, nestas condições o tamanho do mercado de cada classe de carro. Carros acima de R$ 116 mil tem cerca de 1% da população como mercado, carros até R$ 78 mil tem cerca de 5%, carros até R$ 41 mil tem cerca de 14% do mercado, carros até R$ 24 mil tem até 29% do mercado e carros até R$ 14 mil tem até 50% do mercado.

Isto quer dizer, em um universo de 200 milhões de pessoas ou 60 milhões de famílias, poderíamos suportar algo na faixa de 30 milhões de carros. Isto claro que são carros novos. Considerando carros usados, este número pode muito bem dobrar.

O número atual no Brasil é de 50 milhões de carros.

Nada mal para um exercício de conta...

Quando 51 é 40

Um ponto muito interessante da estatística é o chamado intervalo de confiança

Efetivamente, na estatística se assume a aleatoriedade na escolha da amostra e outras coisas mais. Mas o importante é:

O tamanho da amostra é de fundamental importância na estimativa do resultado. Isso ainda depende da distribuição em si. Mas para simplificar vamos dizer que as distribuições envolvidas são normais.

Neste caso, vamos considerar uma eleição aonde temos um dos candidatos com 49% e o outro com 51%. Queremos saber as faixas de proporção dado o intervalo de confiança e o tamanho da população.

Assim para um intervalo de 90%
- para uma amostra com 10 pessoas - 51% está na realidade entre 25 e 77%
- para uma amostra com 20 pessoas - 51% está na realidade entre 32 e 69%
- para uma amostra com 40 pessoas - 51% está na realidade entre 38 e 64%
- para uma amostra com 80 pessoas - 51% está na realidade entre 41 e 60%
- para uma amostra com 160 pessoas - 51% está na realidade entre 44 e 57%
- para uma amostra com 320 pessoas - 51% está na realidade entre 46 e 55%
- para uma amostra com 640 pessoas - 51% está na realidade entre 47 e 54%
- para uma amostra com 1280 pessoas - 51% está na realidade entre 48 e 53%
- para uma amostra com 2560 pessoas - 51% está na realidade entre 49 e 52%
- para uma amostra com 5120 pessoas - 51% está na realidade entre 49 e 52%
- para uma amostra com 10240 pessoas - 51% está na realidade entre 50 e 51.8%

Portanto com um intervalo de 90% só podemos chegar a algo na vizinhança de 51% com mais de 10.000 pessoas na amostra.

Já para o intervalo de 99% isto só é possível com um intervalo de 20480 pessoas.

Então muito cuidado nas pesquisas, elas só contam uma aproximação da realidade

Conta de padeiro

Estes exemplos são o que conheço como "conta de padeiro"

Essencialmente, no equilíbrio tudo que entra deve sair. Isto é na realidade um sistemas de equações de fluxo.

O dinheiro que circula não pode surgir do nada. De modo similar nem a mercadoria. Se alguma das partes não fizer o seu papel, então todo o sistema deixa de funcionar.

Se o produtor resolver acumular capital, como consequência irá deixar alguma das partes sem capital. O resultado é que esta falta de capital irá se refletir novamente no produtor - sob a forma de excesso de mercadorias. O que vimos nos exemplos é que o perdedor imediato é o varejista.

Como ele não é bobo, iria tentar compensar suas perdas na próxima compra com o produtor. E aí ele se viria sob ataque.

O sistema também dá indicações de onde o capital pode crescer: somente quando existe um mercado a ser aproveitado. Em outras palavras, na fase de crescimento o sistema pode realmente proporcionar ganhos aos envolvidos.

Assim desde que o produtor consiga vender suas mercadorias e acumular capital com elas, e desde que o varejista sempre tenha um mercado em expansão então o acúmulo de capital é possível.

Na realidade existe outra situação: quando há concorrência e o mercado envolve diversos atores (vários setores de banco, trabalhadores e produtores). Então através de ganhos diferenciais no mercado (o que caracteriza uma expansão do mercado) o produtor e mesmo o varejista podem acumular capital.

Vamos a um exemplo com expansão com apenas trabalhadores, outros consumidores, um produtor, um varejista e um banqueiro.

Momento 0:

Produtor
- Recebe 2200 do banqueiro para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 1000 itens
- Recebe 3500 do varejista A em troca de 1000 itens
- Paga 2250 ao banqueiro
- Paga 50 ao varejista na compra de 125/11 itens de A
Acúmulo total: 2200-2200+3500-2250-50=1200

Varejista
- Recebe 3500 do banqueiro
- Paga 3500 ao produtor A em troca de 1000 itens
- Recebe 2200 dos trabalhadores em troca de 500 itens
- Recebe 50 do banqueiro em troca de 125/11 itens (11.36 itens)
- Recebe 50 do produtor em troca de 125/11 itens (11.36 itens)
- Recebe 2100 dos consumidores em troca de 5250/11 itens (477.27 itens)
- Paga 3550 ao banqueiro
Acúmulo tota: 3500-3500+2200+50+50+2100-3550=850

Momento 1:

Produtor
- Recebe 1000 do banqueiro para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 1000 itens
- Recebe 3500 do varejista A em troca de 1000 itens
- Paga 1050 ao banqueiro
- Paga 50 ao varejista na compra de 125/11 itens de A
Acúmulo total: 1200+1000-2200+3500-1050-50=2400

Varejista
- Recebe 2650 do banqueiro
- Paga 3500 ao produtor A em troca de 1000 itens
- Recebe 2200 dos trabalhadores em troca de 500 itens
- Recebe 50 do banqueiro em troca de 125/11 itens (11.36 itens)
- Recebe 50 do produtor em troca de 125/11 itens (11.36 itens)
- Recebe 2100 dos consumidores em troca de 5250/11 itens (477.27 itens)
- Paga 2700 ao banqueiro
Acúmulo tota: 850+2650-3500+2200+50+50+2100-2700=1700

E assim sucessivamente. Note que não há sinal de aumento da exploração dos trabalhadores, o que mudou foi uma classe adicional de consumidores.

Ao se estabilizar fixa-se o patamar de operação

E o que acontece com a mais valia?

Neste exemplo, a mais valia pode ser representada simplesmente pelo aumento da quantidade de itens na fábrica.

Então na empresa A ao invés de termos 1000 itens fabricados ao custo de 2300 (2200 dos trabalhadores, 50 para o banqueiro A e 50 para o produtor), teremos 2000 itens fabricados ao custo de 2300.

Consideramos a mesma situação na fábrica B (10000 itens ao invés de 5000).

Então o que muda? Exclusivamente o custo final da mercadoria - que fica mais barato. Os trabalhadores compram mais, os banqueiros compram mais e os produtores compram mais.

Vamos ao exemplo:

ANTES DO AUMENTO DE MAIS VALIA

Produtor A

- Recebe 2200 do banqueiro A para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 1000 + 125/6 itens
- Recebe 2300 do varejista A em troca de 1000 itens
- Paga 2250 ao banqueiro A
- Paga 50 ao varejista B na compra de 625/6 itens de B
Total final: 2200-2200+2300-2250-50 = 0


Produtor B
- Recebe 2200 do banqueiro A para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 5000 + 625/6 itens
- Recebe 2300 do varejista B em troca de 5000 itens
- Paga 2250 ao banqueiro A
- Paga 50 ao varejista A na compra de 125/6 itens de A
Total final: 2200-2200+2300-2250-50 = 0

Varejista A
- Recebe 2300 do banqueiro B
- Paga 2300 ao produtor A em troca de 1000 itens
- Recebe 2200 dos trabalhadores em troca de 5500/6 itens (916.67 itens)
- Recebe 50 do varejista B em troca de 125/6 itens (20.83 itens)
- Recebe 50 do banqueiro A em troca de 125/6 itens (20.83 itens)
- Recebe 50 do banqueiro B em troca de 125/6 itens (20.83 itens)
- Recebe 50 do produtor B em troca de 125/6 itens (20.83 itens)
- Paga 2350 ao banqueiro B
- Paga 50 ao varejista B em troca de 625/6 itens (104.17 itens)
Total final: 2300-2300+2200+50+50+50+50-2350-50=0

Varejista B
- Recebe 2300 do banqueiro B
- Paga 2300 ao produtor B em troca de 5000 itens
- Recebe 2200 dos trabalhadores em troca de 27500/6 itens (4583.33 itens)
- Recebe 50 do varejista A em troca de 625/6 itens (104.17 itens)
- Recebe 50 do banqueiro A em troca de 625/6 itens (104.17 itens)
- Recebe 50 do banqueiro B em troca de 625/6 itens (104.17 itens)
- Recebe 50 do produtor A em troca de 625/6 itens (104.17 itens)
- Paga 2350 ao banqueiro B
- Paga 50 ao varejista A em troca de 125/6 itens (20.83 itens)
Total final: 2300-2300+2200+50+50+50+50-2350-50=0

Trabalhador A
- Recebem 2200 do produtor A
- Paga 1100 ao varejista A em troca de 5500/6 itens
- Paga 1100 ao varejista B em troca de 27500/6 itens
Total final: 2200-1100-1100=0

Trabalhador B
- Recebem 2200 do produtor B
- Paga 1100 ao varejista A em troca de 5500/6 itens
- Paga 1100 ao varejista B em troca de 27500/6 itens
Total final: 2200-1100-1100=0

DEPOIS DO AUMENTO DE MAIS VALIA

Produtor A

- Recebe 2200 do banqueiro A para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 2000 + 125/3 itens
- Recebe 2300 do varejista A em troca de 2000 itens
- Paga 2250 ao banqueiro A
- Paga 50 ao varejista B na compra de 625/3 itens de B
Total final: 2200-2200+2300-2250-50 = 0

Produtor B
- Recebe 2200 do banqueiro A para pagar os trabalhadores
- Paga 2200 aos trabalhadores em troca de 10000 +625/3 itens
- Recebe 2300 do varejista B em troca de 10000 itens
- Paga 2250 ao banqueiro A
- Paga 50 ao varejista A na compra de 125/3 itens de A
Total final: 2200-2200+2300-2250-50 = 0

Varejista A
- Recebe 2300 do banqueiro B
- Paga 2300 ao produtor A em troca de 2000 itens
- Recebe 2200 dos trabalhadores em troca de 5500/3 itens (1833.33 itens)
- Recebe 50 do varejista B em troca de 125/3 itens (41.67 itens)
- Recebe 50 do banqueiro A em troca de 125/3 itens (41.67 itens)
- Recebe 50 do banqueiro B em troca de 125/3 itens (41.67 itens)
- Recebe 50 do produtor B em troca de 125/3 itens (41.67 itens)
- Paga 2350 ao banqueiro B
- Paga 50 ao varejista B em troca de 625/3 itens (208.33 itens)
Total final: 2300-2300+2200+50+50+50+50-2350-50=0

Varejista B
- Recebe 2300 do banqueiro B
- Paga 2300 ao produtor B em troca de 10.000 itens
- Recebe 2200 dos trabalhadores em troca de 27500/3 itens (9166.67 itens)
- Recebe 50 do varejista A em troca de 625/3 itens (208.33 itens)
- Recebe 50 do banqueiro A em troca de 625/3 itens (208.33 itens)
- Recebe 50 do banqueiro B em troca de 625/3 itens (208.33 itens)
- Recebe 50 do produtor A em troca de 625/3 itens (208.33 itens)
- Paga 2350 ao banqueiro B
- Paga 50 ao varejista A em troca de 125/3 itens (41.67 itens)
Total final: 2300-2300+2200+50+50+50+50-2350-50=0

Trabalhador A
- Recebem 2200 do produtor A
- Paga 1100 ao varejista A em troca de 5500/3 itens
- Paga 1100 ao varejista B em troca de 27500/3 itens
Total final: 2200-1100-1100=0

Trabalhador B
- Recebem 2200 do produtor B
- Paga 1100 ao varejista A em troca de 5500/3 itens
- Paga 1100 ao varejista B em troca de 27500/3 itens
Total final: 2200-1100-1100=0

Então o efeito real em um sistema fechado é muito diverso do que o antevisto por Marx. Portanto a mais valia sozinha não pode causar acumulação de capital

Outro mecanismo de acumulação

Se os produtores A e B venderem tudo sem consumir e só acumulando dinheiro:

Ambos tem de pegar 2200,00 com o banco. Mas o produtor A vende 1000 itens por 2300,00. Já o produtor B vende 5000 itens por 2300,00.

Do lado varejista, o varejista A tem de pegar no banco 2300,00 por 1000 mercadorias. Já o varejista B tem de pegar 2300,00 por 5000 mercadorias.

Então A terá de vender 980 itens por 2400,00 e B terá de vender 4900 itens por 2400,00

O custo final da mercadoria será:

A - 2400/980 = 120/49 = 2.45
B - 2400/4900 = 24/49 = 0.49

Como os trabalhadores só possuem 100 para gastos então terão de comprar mais. Para simplificar, vamos supor que os bens podem ser divididos em unidades menores

50/(120/49) = 245/12 itens
50/(24/49) = 1225/12 itens

Logo para o varejista:


Caso B:
Trabalhadores: 1225/12*24/49 x 44 = 2200
Banqueiro A: 1225/12*24/49 = 50
Banqueiro B: 1225/12*24/49 = 50
Total: 2300,00

Ele ainda deve 50,00 ao Banqueiro B tem em excesso 2*1225/12*24/49 itens

O mesmo acontece para o caso A

Assim o varejista acaba pagando pela acumulação do produtor.

E se só um produtor aumentar seu retorno?

Neste caso vamos dizer que o produtor A quer 100,00, mas o produtor B está satisfeito com os 50,00

Ambos tem de pegar 2200,00 com o banco. Mas o produtor A vende 980 itens por 2350,00. Já o produtor B vende 4900 itens por 2300,00.

Do lado varejista, o varejista A tem de pegar no banco 2350,00 por 980 mercadorias. Já o varejista B tem de pegar 2300,00 por 4900 mercadorias.

Então A terá de vender 960 itens por 2450,00. Já B terá de vender 4800 itens por 2400,00.

O custo final da mercadoria será:

A - 2450/960 = 245/96 = 2.55
B - 2400/4800 = 0.5

De forma igual os trabalhadores só possuem 100 para gastos e portanto terá de comprar menos da mercadoria A (960/49 itens), mas a mesma coisa da mercadoria B (2200). Então teremos:

Caso B:

Trabalhadores: 4800/50*50/96 x 44 = 2200
Banqueiro A: 4800/50*50/96 = 50
Banqueiro B: 4800/50*50/96 = 50
Produtor A: 2*4800/50*50/96 = 100
Total: 2400,00

Pago ao banco: 2350,00

Portanto ele tem 50,00 para comprar mercadoria de A.

Caso A:
Trabalhadores: 960/49*245/96 x 44 = 2200
Banqueiro A: 960/49*245/96 = 50
Banqueiro B: 960/49*245/96 = 50
Produtor B: 960/49*245/96 = 50
Varejista B: 960/49*245/96 = 50
Total: 2400,00

Pago ao Banco: 2400,00

Sobra para ele 960/49 itens A. Infelizmente ele não poderá trocar com o varejista B pois ele não tem mais mercadorias.

Neste caso a solução lógica é comprar menos elementos da próxima vez. E aí é o produtor A que saí perdendo (ele pode transferir isto para os empregados pagando menos, mas aí o sistema todo passa a sofrer).

O que fica claro destes exemplos é: o ganho pelo aumento de preço simples não se sustenta no longo prazo - a não ser que todos os produtores o pratiquem. Isto apenas torna mais cara a mercadoria a ser vendida no sistema e força os varejistas a recorrem ao escambo para se sustentar.

Portanto, neste modelo o aumento de preços não funciona muito bem como mecanismo de acumulação de capital

Mais do Modelo

Agora podemos começar a brincar com o modelo.

Vamos dizer que o produtor está insatisfeito com os 50,00 que recebe por tanto trabalho. Agora ele quer 100,00

Então, tem de pegar com o banco 2200,00, pagar os empregados e vender 980 mercadorias (ou 4900) por 2350,00. E por fim pagar ao banco 2250,00 e compra 100,00 de mercadoria do varejista.

Do lado do varejista, ele tem de pegar no banco 2350,00 por 980 mercadorias (ou 4900) e pagar ao produtor 2350,00. Já ele terá de vender 960 mercadorias (ou 4800) por R$ 2450,00. Ao final ele paga ao banco 2400,00 e compra 50,00 de mercadoria do outro varejista.

O custo final da mercadoria será:
A - 2450/960 = 245/96 = 2.55
B - 2450/4800 = 49/96 = 0.51

Como os trabalhadores só possuem 100 para gastos então terão de comprar menos. Para simplificar, vamos supor que os bens podem ser divididos em unidades menores

50/(245/96) = 960/49 itens
50/(49/96) = 4800/49 itens

Logo para o varejista:


Caso B:
Trabalhadores: 4800/49*49/96 x 44 = 2200
Banqueiro A: 4800/49*49/96 = 50
Banqueiro B: 4800/49*49/96 = 50
Produtor A: 2*4800/49*49/96 = 100
Total: 2400,00

Pago ao Banco: 2400,00

Mercadoria B sobrando na mão do varejista: 4800/49

- Para compensar ele pode trocar 4800/49 de B por 960/49 de mercadoria com o varejista A


Caso A:
Trabalhadores: 960/49*245/96 x 44 = 2200
Banqueiro A: 960/49*245/96 = 50
Banqueiro B: 960/49*245/96 = 50
Produtor B: 2*960/49*245/96 = 100
Total: 2400,00

Pago ao Banco: 2400,00

Mercadoria A sobrando na mão do varejista: 960/49

- Para compensar ele pode trocar 960/49 de A por 4800/49 de mercadoria com o varejista B

Então:

- O varejista B é forçado a uma poupança - não consumir da mercadoria A ou trocar diretamente mercadoria com mercadoria com o varejista A.

O mesmo vale para o varejista A.


O efeito prático é que os produtores tem de comprar mais mercadoria (do contrário não há vazão para os varejistas) e os demais compram um pouco menos de mercadoria. Ou seja, há um encarecimento aparente das mercadorias.